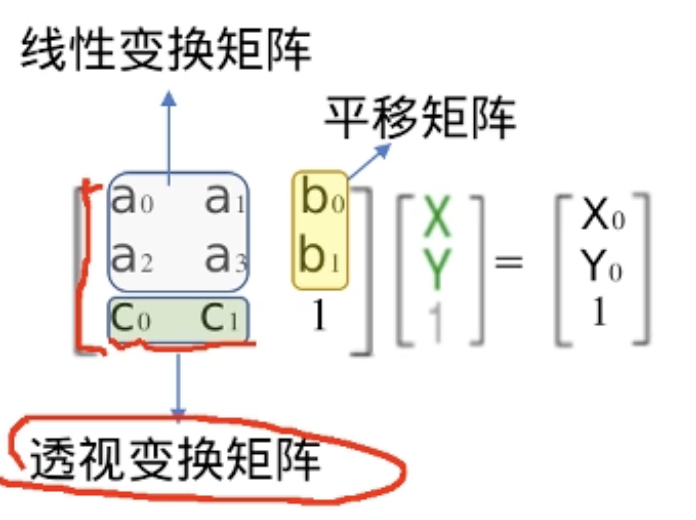
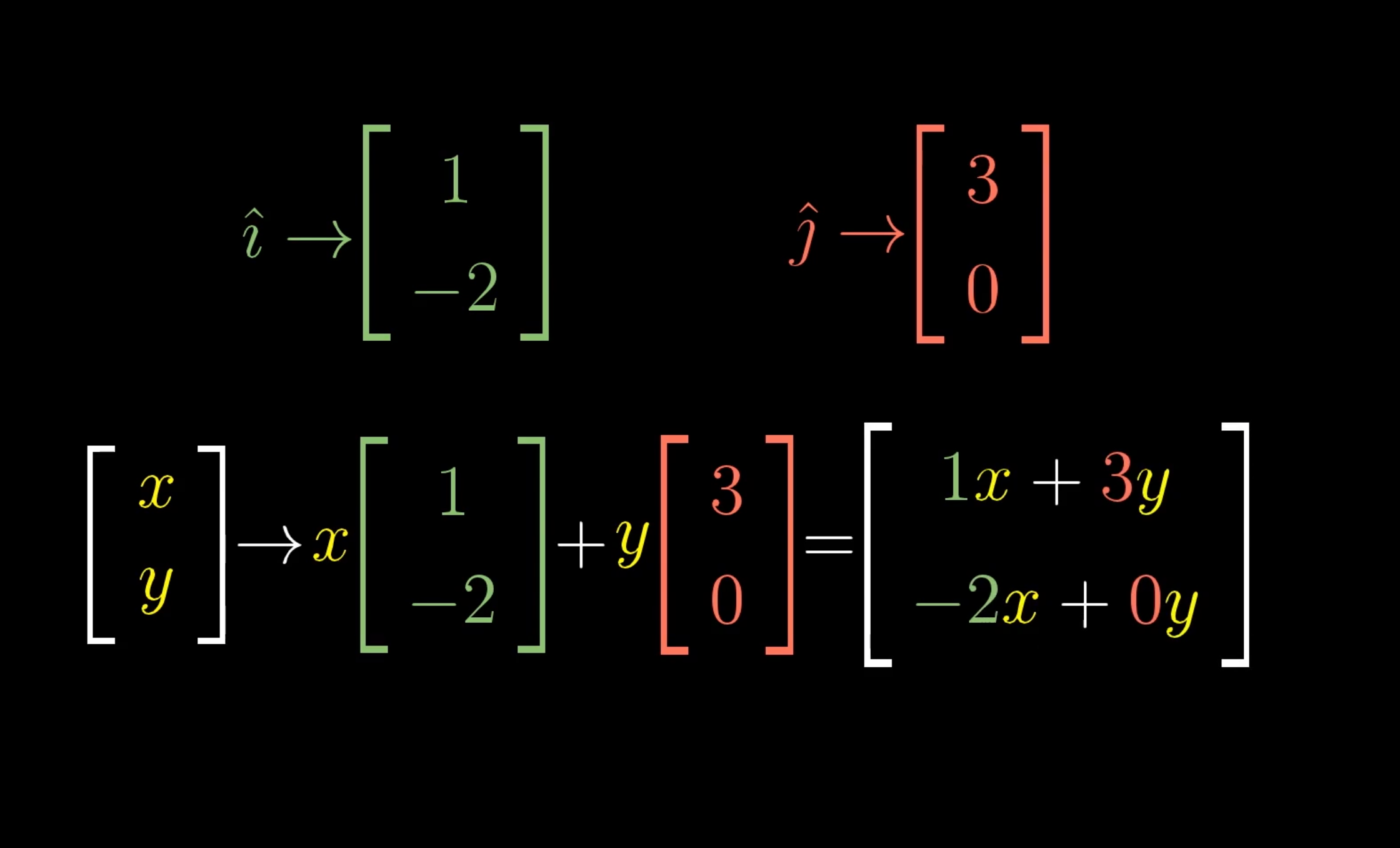在图像处理时第一次遇到透视变换,具体实现使用到矩阵对图像进行处理。对具体数学原理比较好奇,于是重新学习线性代数,这次希望在理解本质上下功夫。
Origin: 3Blue1Brown-EssenceOfLinearAlgbra
Essence of Linear Algbra
Linear Combinations, Span, and Basis Vectors
- Every Vectior is represented vertically(vector coordinates).
- Think of every coordinates as a ‘scaler’ (of the unit vector in either x axis or y axis)
- i and j are the basis vectors of the x&y coordinate system.
- What if we choose differnt basis vectors?
- (a i +b j) is considered the Linear combination of i and j
The “span” of i and j is the set of all their linear combinations. (张成的空间)
When thinking about a single vector, think it as arrow.
while it is a set of vectors, points.If there’s already two vectors while adding the third one dose not change the span of the two (the third vector is redundant), then we can say that they are “Linear dependent”
One of the vector is already in the span of the others’.
This conducts the concept of Linear independent.
Basis of space: a set of linear independent vectors that span the full space.
Linear Transformation and(relations to) Matrices
Transformation ~= Function.
Using the word “Transformation imlies you to concider ‘functions of vectors’ as ‘movement’. (Think as the input vector move over to its corresponding output vector would be intuitive.
Linear Transformation
- Definition
Any types of functions can be applied to any vectors(or the whole vector space). While some Transformations can be complicated, some, as Linear Algbra limits itselves in, are easier to understand and is called “Linear Transformations”.
Linear Transformations:
- Lines remain lines in the vector space.
- Origin remain fixed.
To sum up, in linear transformation, gird lines remain parallel and evenly spaced.- Where’s the vector after the Tranfromation?
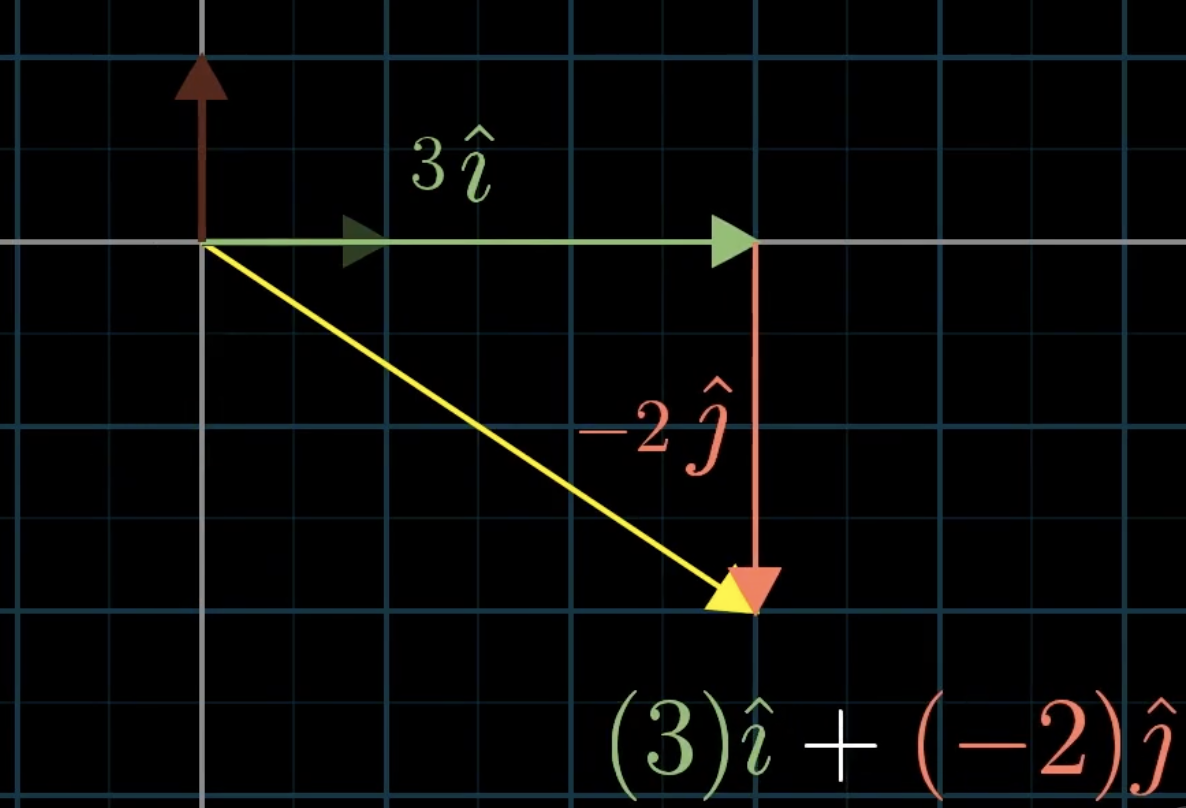
v = -1i + 2j
Transformed v = -1 (Transformed) i + 2 (Transformed) j
Any vector is represented by a linear combination of multiple vectors( or basis of space).
Consequently just track where the basis vectors had gone we can deduce any transformed vectors of the linear combination.
e.g.: any 2d Linear Transformation can be described by two numbers. (in a 2x2 Matrix.)
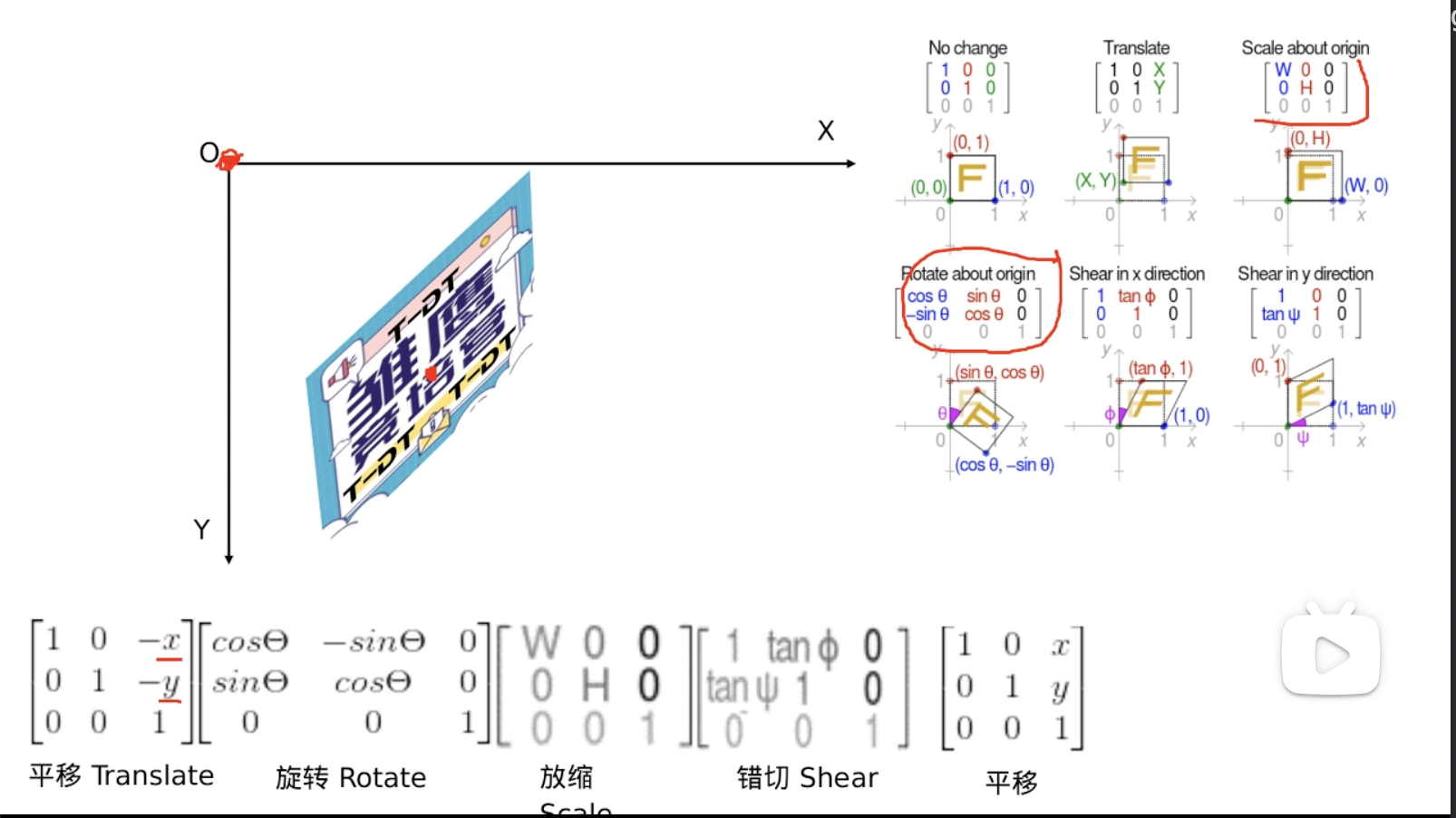
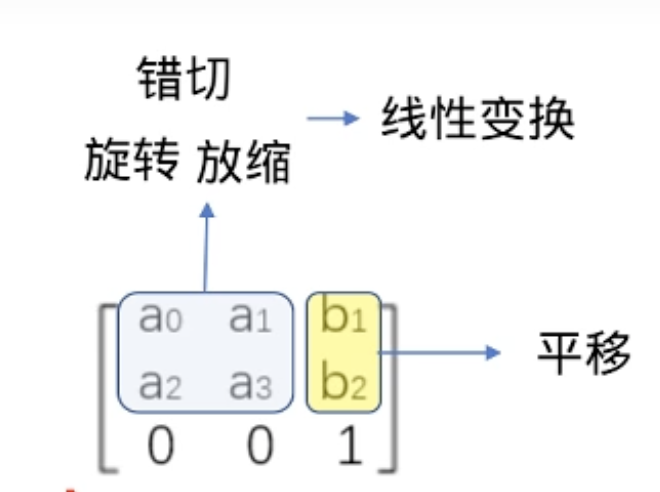
Linear Transformation Application in Image Processing:
仿射变换: